| There are different methods which can be
utilized to find the prime factorization of a number. One way is to
repeatedly divide by prime numbers: |
| |
| EXAMPLE 1. Prime
factorization of 96 (by division): |
96 ÷
2 = 48
48 ÷ 2 = 24
24 ÷ 2 = 12
12 ÷ 2 = 6
6 ÷ 2 = 3
3 ÷ 3 = 1
96 = 2 * 2 * 2 * 2 * 2 * 3 |
| |
| EXAMPLE 2. Prime
factorization of 120 (by division): |
120 ÷
2 = 60
60 ÷ 2 = 30
30 ÷ 2 = 15
15 ÷ 3 = 5
5 ÷ 5 = 1
120 = 2 * 2 * 2 * 3 * 5 |
| |
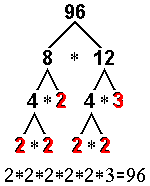
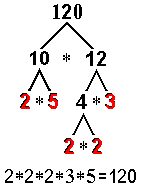
| Another way to approach the task is to
choose ANY pair of factors and split these factors until all the
factors are prime: |
|
 |
 |
| |
Traditionally, the factors are listed in
order from least to greatest.
While the product would be the same regardless of
the order of the factors, it is much easier to compare or evaluate
expressions if the factors are listed in this order.
|
| |
| Determining the prime factors can be
challenging. While it's good to know HOW to do it, on most
standardized tests you'll only have to select the one right answer
choice to show that you understand the concept. |
| |
The CORRECT answer:
must be only PRIME numbers
must multiply together to give the specified quantity. |